Khi bé, bạn đi nhà trẻ. Lớn lên, bạn phải lấy vợ. Kiểu gì cũng không tránh được, trừ các vĩ nhân.
Chuyện lấy vợ ngày xưa rất đơn giản. Một ngày đẹp trời, bố khề khà nói với…mẹ “Tôi xem con Sứt con ông phó cối đầu ngõ chăm chỉ đáo để….” Thế là vài tháng sau bạn sẽ là chồng của cô Sứt, và ngày ngày đóng cối….
Chuyên bây giờ không đơn giản như thế nữa. Bạn có tự do, có quyền theo đuổi tình yêu, chắp cánh bay xa, vv. Phải lấy người mình yêu, chà !
Trớ trêu, người bạn yêu (như Angelina Jolie) thì vô số bạn khác cũng yêu. Thế mới cáu. Nhưng không sao, chuyện này các ông Tây cũng đã nghĩ tới, chẳng phải vì cô Angelina là Tây, mà ở bên Tây luật một vợ một chồng có sớm hơn ta, nên các bác ấy phải đi trước một bước, âu cũng là cực chẳng đã.
Các ông Tây giải quyết vấn đề như sau: Thay vì mỗi Angelina, mỗi ông lên một danh sách gồm các cô có thể đưa vào tầm ngắm. Danh sách này sẽ ngắn dài gầy béo tùy theo khả năng và sở thích mối người. Câu hỏi đặt ra là: Khi nào bạn có thể lấy được một
người trong danh sách của bạn mà không dẫn đến một cuộc đọ súng đọ kiếm hay đọ một cái gì với các bạn khác ?
Điều kiện cần của bài toán tương đối dễ xác định. Tưởng tượng cô Mít và cô Đào rất “hot”, và là ý trung nhân của các anh Mai, Thuổng và Xẻng. Thế là hai thục nữ nhưng những ba anh hùng, kiếu gì cũng không ổn. Nói tổng quát, nếu danh sách của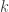 chàng tổng cộng lại chỉ có
chàng tổng cộng lại chỉ có  nàng, thì thế nào cũng dẫn đến mâu thuẫn khó giải quyết. Vậy điều kiện cần của bài toán Lấy (một trong những) Người Mình Yêu là:
nàng, thì thế nào cũng dẫn đến mâu thuẫn khó giải quyết. Vậy điều kiện cần của bài toán Lấy (một trong những) Người Mình Yêu là:
(1) Vơi mọi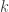 , danh sách của bât kỳ
, danh sách của bât kỳ 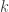 chàng trai nào tổng cộng lai phải có ít nhất
chàng trai nào tổng cộng lai phải có ít nhất 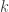 cô gái.
cô gái.
Định lý Lấy Người Mình Yêu của Hall (Hall Marriage’s thẻoem) nói rằng đây cũng là điều kiện đủ.
Định lý Hall (1) là điều kiện đủ.
Đjinh lý này có thể phảt biểu dươi dạng đồ thị. Ta biểu diễn các chàng trai bằng chấm màu đỏ và các cô gái bằng chấm màu xanh. Đồ thị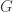 có các cạnh giữa chấm xanh và chấm đỏ,
có các cạnh giữa chấm xanh và chấm đỏ,  nối với
nối với 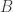 nếu nàng
nếu nàng 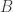 ở trong danh sách của chàng
ở trong danh sách của chàng  . Một “perfect matching” là một tập các cạnh không dính nhau phủ hết các đỉnh đỏ.
. Một “perfect matching” là một tập các cạnh không dính nhau phủ hết các đỉnh đỏ.
Định lý Hall.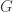 có perfect matching khi và chỉ khi vơi mọi
có perfect matching khi và chỉ khi vơi mọi 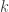 , với mọi tập đỏ
, với mọi tập đỏ 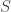 với
với 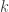 phần tử, số đỉnh xanh nối vởi
phần tử, số đỉnh xanh nối vởi 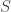 ít nhất là
ít nhất là 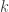 .
.
Định lý Hall chứng minh không khó, bạn có thể thử dưới dạng bài tập. Trong phần còn lại của bài, ta sẽ dùng định lý Hall để chứng minh một trong những định lý quan trọng nhất trong đại số tuyến tính: định lý Birkoff. Để phát biếu định lý này, ta cần một khái niệm. Một ma trận được gọi là doubly stochastic nếu các phần tử là số không âm và tổng mối hàng và mỗi cột là một. Nếu ta biếu diễn ma trận đưới dạng một điểm trong không gian
được gọi là doubly stochastic nếu các phần tử là số không âm và tổng mối hàng và mỗi cột là một. Nếu ta biếu diễn ma trận đưới dạng một điểm trong không gian  thì các ma trận DS tạo thành một tập lồi; chính xác hơn, một đa diện lồi
thì các ma trận DS tạo thành một tập lồi; chính xác hơn, một đa diện lồi 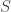 . Câu hỏi đặt ra là: tìm đỉnh của đa diện này. Câu hỏi này quan trọng, vì trong rất nhiều bài toán cực trị, giá trị cực trị được đạt được trên các đỉnh.
. Câu hỏi đặt ra là: tìm đỉnh của đa diện này. Câu hỏi này quan trọng, vì trong rất nhiều bài toán cực trị, giá trị cực trị được đạt được trên các đỉnh.
Birkoff tìm ra câu trả lời rất đẹp cho câu hỏi này. Một ma trận DS được gọi là “permutation matrix” nếu mỗi hàng và mỗi cột có chính xác một số một (còn lại là không). Bạn có thể dễ dàng thấy rằng mối PM tương đương với một phần tử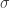 của nhóm giao hoán
của nhóm giao hoán 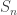 . Bạn cũng có thể dễ dàng chứng minh các PM là đỉnh của đa diện
. Bạn cũng có thể dễ dàng chứng minh các PM là đỉnh của đa diện 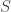 . Birkoff chứng minh rằng ngoài ra không còn đỉnh nào khác.
. Birkoff chứng minh rằng ngoài ra không còn đỉnh nào khác.
Định lý Birkoff. Tập PM là các đỉnh duy nhất của đa diện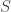 .
.
Giả sử là một ma trận với phần tử
là một ma trận với phần tử  . Với mỗi giao hoán
. Với mỗi giao hoán 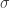 , ta gọi dãy
, ta gọi dãy  là một diagonal của
là một diagonal của  . Bạn có thể dùng định lý Hall để chứng minh bổ đề sau
. Bạn có thể dùng định lý Hall để chứng minh bổ đề sau
{ Bổ đề.} Nếu mỗi diagonal của có ít nhất một số
có ít nhất một số 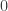 thì
thì  có một
có một  ma trận con với các phần tử đều bằng
ma trận con với các phần tử đều bằng 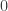 và
và  .
.
Chứng minh định lý Birkoff. Giả sử là một điểm trong
là một điểm trong 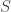 . Ta sẽ chứng minh
. Ta sẽ chứng minh  có thể viết đưới dạng
có thể viết đưới dạng  , với
, với  và
và  là PM. Ta qui nạp theo số phần tử dương của
là PM. Ta qui nạp theo số phần tử dương của  . Nếu
. Nếu  có
có  phần tử dương thì nó là một PM. Giả sử
phần tử dương thì nó là một PM. Giả sử  có
có  phần tử dương. Bạn có thể dễ dàng kiểm tra là một ma trận DS không thể có một ma trận con như trong bổ đề (bài tập). Như vậy, ta có một diagonal gồm toàn số dương. Diagonal này gắn với một phép giao hoán
phần tử dương. Bạn có thể dễ dàng kiểm tra là một ma trận DS không thể có một ma trận con như trong bổ đề (bài tập). Như vậy, ta có một diagonal gồm toàn số dương. Diagonal này gắn với một phép giao hoán 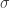 , và qua đó, một PM
, và qua đó, một PM 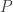 . Gọi
. Gọi  là giá trị (dương) nhỏ nhất trong diagonal trên và
là giá trị (dương) nhỏ nhất trong diagonal trên và 
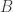 cũng là một DS matrix. Ngoài ra sồ phần tử dương của nó
cũng là một DS matrix. Ngoài ra sồ phần tử dương của nó  . Vậy
. Vậy 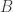 có thể biểu diến dưới dạng
có thể biểu diến dưới dạng  . Nhưng,
. Nhưng,  . QED
. QED
Chuyện lấy vợ ngày xưa rất đơn giản. Một ngày đẹp trời, bố khề khà nói với…mẹ “Tôi xem con Sứt con ông phó cối đầu ngõ chăm chỉ đáo để….” Thế là vài tháng sau bạn sẽ là chồng của cô Sứt, và ngày ngày đóng cối….
Chuyên bây giờ không đơn giản như thế nữa. Bạn có tự do, có quyền theo đuổi tình yêu, chắp cánh bay xa, vv. Phải lấy người mình yêu, chà !
Trớ trêu, người bạn yêu (như Angelina Jolie) thì vô số bạn khác cũng yêu. Thế mới cáu. Nhưng không sao, chuyện này các ông Tây cũng đã nghĩ tới, chẳng phải vì cô Angelina là Tây, mà ở bên Tây luật một vợ một chồng có sớm hơn ta, nên các bác ấy phải đi trước một bước, âu cũng là cực chẳng đã.
Các ông Tây giải quyết vấn đề như sau: Thay vì mỗi Angelina, mỗi ông lên một danh sách gồm các cô có thể đưa vào tầm ngắm. Danh sách này sẽ ngắn dài gầy béo tùy theo khả năng và sở thích mối người. Câu hỏi đặt ra là: Khi nào bạn có thể lấy được một
người trong danh sách của bạn mà không dẫn đến một cuộc đọ súng đọ kiếm hay đọ một cái gì với các bạn khác ?
Điều kiện cần của bài toán tương đối dễ xác định. Tưởng tượng cô Mít và cô Đào rất “hot”, và là ý trung nhân của các anh Mai, Thuổng và Xẻng. Thế là hai thục nữ nhưng những ba anh hùng, kiếu gì cũng không ổn. Nói tổng quát, nếu danh sách của
(1) Vơi mọi
Định lý Lấy Người Mình Yêu của Hall (Hall Marriage’s thẻoem) nói rằng đây cũng là điều kiện đủ.
Định lý Hall (1) là điều kiện đủ.
Đjinh lý này có thể phảt biểu dươi dạng đồ thị. Ta biểu diễn các chàng trai bằng chấm màu đỏ và các cô gái bằng chấm màu xanh. Đồ thị
Định lý Hall.
Định lý Hall chứng minh không khó, bạn có thể thử dưới dạng bài tập. Trong phần còn lại của bài, ta sẽ dùng định lý Hall để chứng minh một trong những định lý quan trọng nhất trong đại số tuyến tính: định lý Birkoff. Để phát biếu định lý này, ta cần một khái niệm. Một ma trận
Birkoff tìm ra câu trả lời rất đẹp cho câu hỏi này. Một ma trận DS được gọi là “permutation matrix” nếu mỗi hàng và mỗi cột có chính xác một số một (còn lại là không). Bạn có thể dễ dàng thấy rằng mối PM tương đương với một phần tử
Định lý Birkoff. Tập PM là các đỉnh duy nhất của đa diện
Giả sử
{ Bổ đề.} Nếu mỗi diagonal của
Chứng minh định lý Birkoff. Giả sử
Homework for combinatorics 1 (part 2)
(1) Let 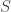 be a set of at least
be a set of at least  points in
points in  . Prove that
. Prove that 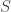 can be partitioned into two subsets whose convex hulls intersect.
can be partitioned into two subsets whose convex hulls intersect.
(2) Let be convex sets in
be convex sets in  such that any
such that any  of them intersect. Prove that all of them intersect.
of them intersect. Prove that all of them intersect.
(3) Let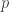 be a fixed prime. Construct a family of
be a fixed prime. Construct a family of  subsets of
subsets of  such that each has cardinality
such that each has cardinality  but any two has intersection
but any two has intersection
either 0, 1,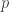 or
or  .
.
(4)* Let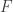 be a family of subsets of
be a family of subsets of  such that the intersection of any three is even. Prove that for all sufficiently large
such that the intersection of any three is even. Prove that for all sufficiently large  ,
,  .
.
(*) is a bonus problem, it does not count if you cannot do it, but if you can, I am willing to hear the solution.
(2) Let
(3) Let
either 0, 1,
(4)* Let
(*) is a bonus problem, it does not count if you cannot do it, but if you can, I am willing to hear the solution.

Không có nhận xét nào:
Đăng nhận xét